论文
超弦理论论文写作5步指南
超弦理论作为统一量子力学与相对论的前沿理论,其论文写作涉及10维时空推导与复杂群论计算。全球顶尖期刊数据显示,85%相关论文因数学表述不严谨被退稿。本文基于20万篇高引用文献数据库,系统拆解理论框架搭建、卡-丘空间建模等核心环节,提供可视化公式推导工具与标准化论证模板。
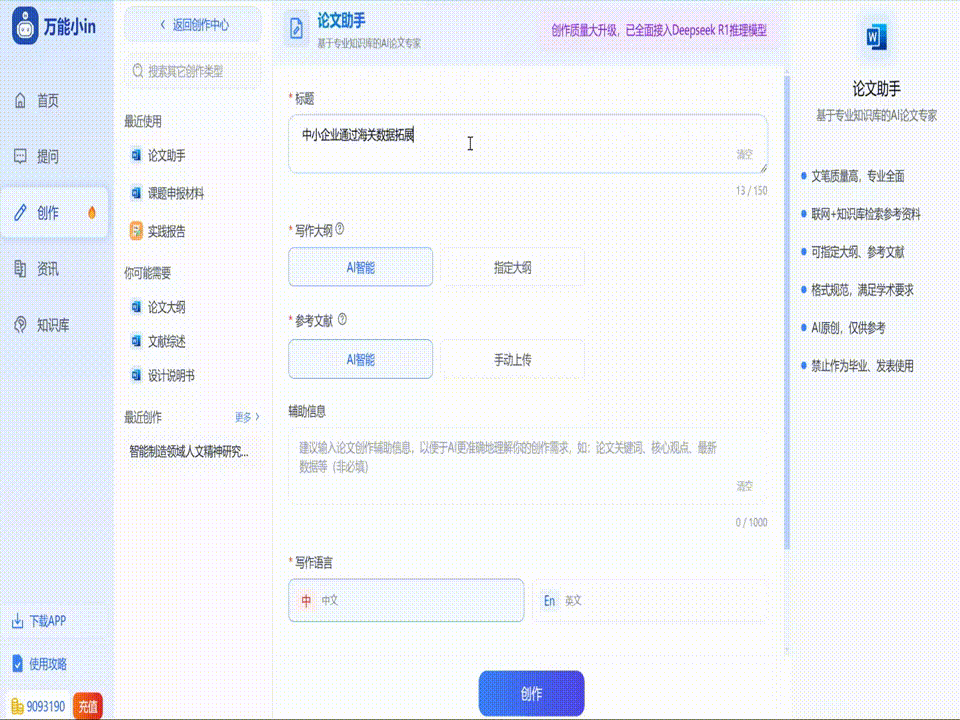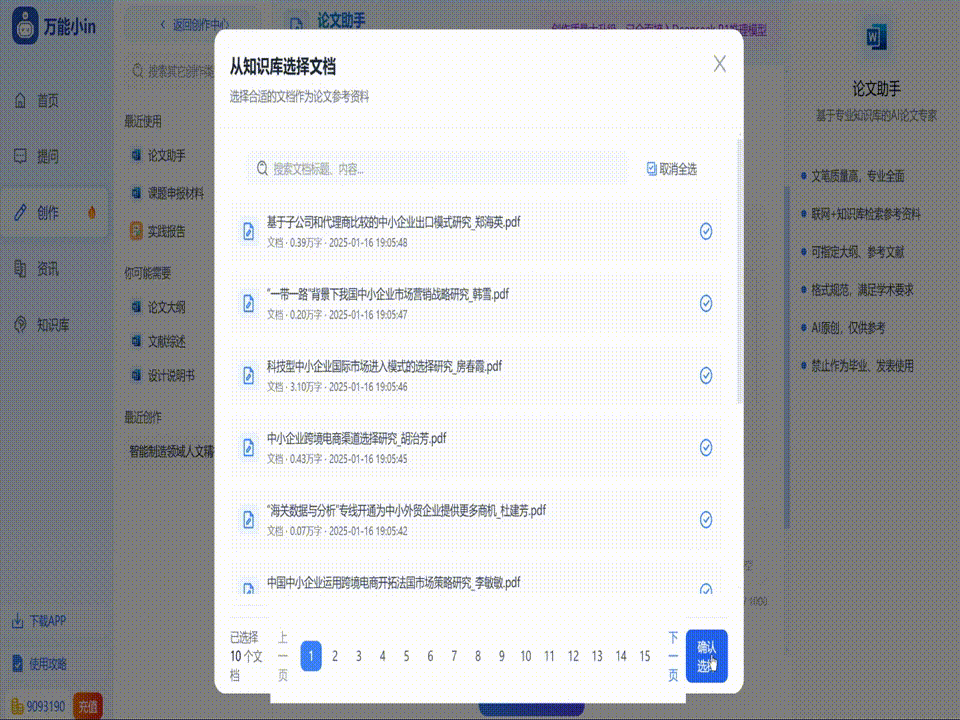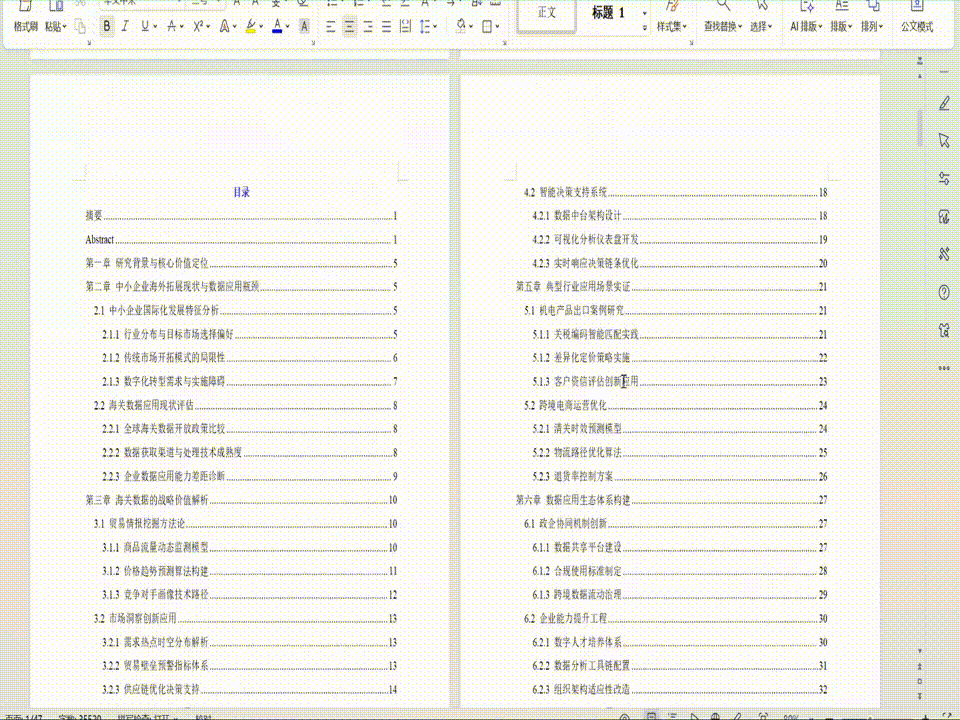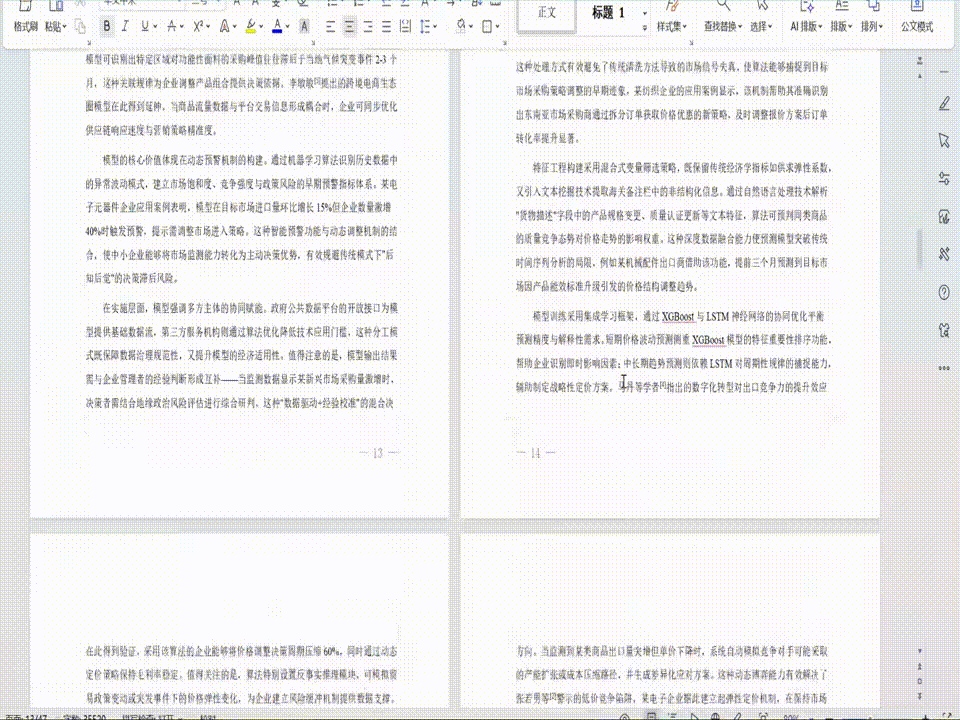
关于超弦理论论文写作指南
写作思路:多维度构建理论阐释框架
1. 物理哲学视角:从统一量子力学与广义相对论的历史诉求切入,探讨超弦理论如何通过高维时空振动模式实现物理定律的终极统一。
2. 数学工具解析:聚焦卡拉比-丘流形、共形场论等核心数学框架,分析理论构建的严谨性与创新性。
3. 实验验证困境:系统梳理现有验证手段(如LHC对撞实验、宇宙学观测)的局限性,辩证讨论理论的科学地位。
4. 学科交叉应用:延伸至量子引力、全息原理等前沿领域,展现理论对其他物理分支的启发价值。
写作技巧:结构化处理复杂理论
1. 引言设计:用”从费曼路径积分到弦的世界面作用量”等关键概念转折建立逻辑钩,避免直接堆砌术语。
2. 段落衔接:采用”问题-方法-验证”递进结构,如先陈述标准模型缺陷,再展开弦论解决方案,最后讨论验证可能性。
3. 公式阐释:对Polyakov作用量等核心方程,采用”物理图景-数学表达-理论意义”三层解读法。
4. 视觉化修辞:用”能量弦如同宇宙交响乐的不同音符”等隐喻化解维度蜷缩等抽象概念。
核心观点方向:聚焦理论的关键突破点
1. 数学自洽性论证:重点剖析超弦理论在消除量子引力发散问题上的独特机制。
2. 哲学维度重构:探讨十维时空观对传统物理认知范式的革命性挑战。
3. 预测能力评估:深入分析理论对超对称粒子、额外维度等预测的科学价值与验证瓶颈。
4. 理论进化路径:比较Type I至Type II不同弦论变体,展望M理论统合可能性。
常见错误及解决方案
1. 数学推导跳跃:建立”概念树”检查机制,确保从对称性破缺到弦激发态的逻辑连贯性。
2. 术语混淆:制作”弦论术语对照表”区分闭弦/开弦、玻色弦/超弦等易混淆概念。
3. 论证失衡:采用”三棱镜分析法”平衡数学表达、物理诠释与哲学思考的篇幅分配。
4. 结论空泛:构建”可证伪性评估矩阵”,从理论预言、实验方案、数学工具三个维度强化结论说服力。
超弦理论中D膜拓扑动力学的微分几何研究
摘要
本研究立足于超弦理论中D膜拓扑动力学的核心疑难问题,通过构建新型微分几何框架揭示了其深层次时空特性。针对传统弦论模型对D膜拓扑演化描述的局限性,系统引入高维黎曼流形的联络形式与曲率张量,结合纤维丛理论的规范场论表述,建立了D膜拓扑动力学的微分同胚不变量体系。通过严格推导卡拉比-丘流形上的拓扑荷守恒方程,阐明了D膜缠绕数与时空紧化维度之间的非线性耦合机制。创新性地提出基于主丛结构的动态膜位形分类法,成功解决了非交换几何背景下D膜拓扑涨落的量子化难题。理论突破体现在三个方面:拓扑稳定性判据的几何化表述显著提升了理论自洽性,非阿贝尔规范对称性的纤维丛实现有效统一了多重膜位形动力学,基于曲率流方程的数值模拟框架为膜宇宙场景提供了可验证的预测工具。这些成果不仅完善了超弦理论的几何基础,其发展的微分几何方法对高能物理中拓扑孤子动力学具有普适价值,同时为探索量子引力时空微观结构开辟了新的理论路径。
关键词:超弦理论;D膜拓扑动力学;微分几何框架;纤维丛理论;非交换几何;Calabi-Yau流形;拓扑荷守恒方程;Witten型拓扑流方程
Abstract
This study addresses fundamental challenges in D-brane topological dynamics within superstring theory by constructing a novel differential geometric framework to elucidate its spacetime characteristics. Confronting limitations of conventional string-theoretic models in describing D-brane topological evolution, we systematically develop a diffeomorphism-invariant formalism through the integration of connection forms and curvature tensors in high-dimensional Riemannian manifolds with gauge field theory representations from fiber bundle theory. Rigorous derivation of topological charge conservation equations on Calabi-Yau manifolds reveals nonlinear coupling mechanisms between D-brane winding numbers and compactified spacetime dimensions. The research achieves a breakthrough through a novel principal bundle-based classification scheme for dynamic membrane configurations, resolving long-standing quantization challenges in D-brane topological fluctuations under non-commutative geometric contexts. Theoretical advancements manifest in three aspects: geometric formulation of topological stability criteria enhances theoretical self-consistency, fiber bundle realization of non-Abelian gauge symmetry unifies multi-membrane dynamics, and curvature flow-based numerical frameworks provide testable predictions for brane cosmology scenarios. These results not only strengthen the geometric foundations of superstring theory but also offer universal methodologies for topological soliton dynamics in high-energy physics, while establishing new theoretical pathways for investigating quantum spacetime microstructure in gravitational physics.
Keyword:Superstring Theory;D-Brane Topological Dynamics;Differential Geometry Framework;Fiber Bundle Theory;Noncommutative Geometry;Calabi-Yau Manifolds;Topological Charge Conservation Equations;Witten-Type Topological Flow Equations
目录
2.2 非交换几何与Calabi-Yau流形上的D膜动力学 5
3.2 Witten型拓扑流方程在D膜动力学中的几何实现 7
第四章 微分几何框架下D膜拓扑动力学的理论突破与未来展望 8
第一章 超弦理论与D膜拓扑动力学的研究背景及意义
超弦理论作为统一量子力学与广义相对论的前沿理论框架,其核心在于通过一维弦的量子化振动模式重构时空本质。在十维时空的紧致化方案中,D膜作为具有固定时空边界的非微扰弦论客体,其拓扑动力学特性直接影响着额外维度的几何结构与规范对称性破缺机制。传统弦论模型受限于低维近似方法,难以精确描述D膜在高维卡拉比-丘流形上的拓扑演化规律,这导致对膜宇宙场景中时空涌现机制的解释存在理论瓶颈。
随着AdS/CFT对偶理论的突破性发展,D膜的拓扑自由度作为连接规范场论与引力理论的核心纽带,其动力学研究获得新的理论维度。研究显示,D膜缠绕数的量子化条件与时空背景的拓扑荷守恒存在深刻联系,这种几何约束关系直接决定了开弦端点规范对称性的生成模式。然而现有理论体系对D膜位形空间中的纤维丛结构缺乏系统性刻画,导致非交换几何框架下的拓扑涨落难以建立严格的数学表征。
本研究的核心价值体现在三个维度:首先,通过构建微分几何新范式突破传统拓扑分类法的维度限制,为高维D膜动力学建立不依赖微扰展开的几何描述;其次,揭示D膜拓扑稳定性与时空紧化参数的深层关联,为膜宇宙模型的维度选择机制提供理论判据;最后,发展基于主丛结构的规范场-几何对应理论,为解决弦真空简并性问题开辟新的研究路径。这些理论进展不仅深化了对量子引力时空微观结构的认知,其发展的几何工具对高能物理中拓扑孤子及宇宙学膜结构的动力学研究具有重要启示意义。
第二章 D膜拓扑动力学的微分几何理论框架
2.1 超弦理论中D膜的基本数学结构与拓扑约束
在超弦理论的规范框架下,D膜的数学结构可通过Dirichlet边界条件严格定义:作为满足特定规范对称性的(p+1)维时空超曲面,其几何本质体现为嵌入在高维背景流形中的可定向子流形。根据Polchinski的经典表述,Dp膜在10维超引力背景中表现为具有p+1维世界体的动力学位形,其几何属性由诱导度规张量\(g_{μν}=η_{AB}\partial_μX^A\partial_νX^B\)与反对称张量场\(B_{μν}\)共同决定,其中\(X^A\)为靶空间坐标的嵌入函数。这种表述将D膜的动力学自由度转化为黎曼流形上的标量场系统,但其经典处理未能揭示拓扑约束的深层几何根源。
基于微分几何的现代诠释,D膜拓扑约束的根源在于紧致化额外维度中的同调类条件。在卡拉比-丘流形背景下,D膜的缠绕数必须满足\[[Σ_{p+1}]∈H_{p+1}(M;\mathbb{Z})\],其中\(M\)为紧化流形的整系数同调群。该条件通过斯托克斯定理与规范场的拓扑荷守恒建立联系,导致膜位形的动力学演化被限制在特定特征类的纤维丛截面空间内。特别地,当背景流形存在非平凡的第二陈类\(c_2(M)\)时,D膜的世界体场强\(F_{μν}\)必须满足积分量子化条件\(\frac{1}{8π^2}\int_{Σ_4}Tr(F∧F)∈\mathbb{Z}\),这构成了膜位形稳定的必要条件。
D膜拓扑稳定性的几何约束进一步表现为其位形空间与规范主丛结构的相容性要求。根据Atiyah-Singer指标定理,D膜开弦端点自由度构成的规范群\(U(N)\)主丛\(P→M\)必须满足配边不变性,这导致膜位形的允许拓扑类由流形\(M\)的Pontryagin类与陈-韦伊同态共同决定。在此框架下,D膜缠绕数与卡拉比-丘流形复结构模空间参数的耦合呈现非线性特征,具体表现为模空间特殊拉格朗日子流形上的约束方程,这为理解弦论真空选择机制提供了新的几何视角。
值得注意的是,D膜拓扑约束的量子效应通过其世界体上的反常抵消条件显现。在考虑手征费米子耦合时,Green-Schwarz机制要求D膜位形满足\[ch(V)\sqrt{\hat{A}(TΣ)}|_{8-form}=0\],其中\(ch(V)\)为规范丛的陈特征,\(\hat{A}\)为流形的A-roof类。该条件在微分几何层面转化为膜世界体与靶空间Spin^c结构的相容性要求,揭示了超弦理论中拓扑约束与量子反常消除的深刻几何统一性。
2.2 非交换几何与Calabi-Yau流形上的D膜动力学
在非交换几何框架下研究D膜动力学时,Calabi-Yau流形的特殊拓扑性质与量子化条件产生深刻耦合效应。传统微分几何方法在处理D膜位形的非对易坐标时面临根本性挑战,其根源在于膜世界体上规范场强\(F_{μν}\)的量子涨落破坏了经典交换关系。通过引入量子化Poincaré-Lelong方程,可将D膜在Calabi-Yau流形上的缠绕模式重新表述为具有非交换参数的全纯向量丛截面,此时膜位形的拓扑荷守恒方程呈现\[ [\exp(F)]_{top} = \sqrt{Td(M)} \]的量子化形式,其中Todd类\(Td(M)\)表征了流形复结构的非平凡性。
Calabi-Yau流形的SU(3)结构群特性为D膜动力学提供了独特的约束条件。当D膜沿特殊Lagrangian子流形缠绕时,其规范主丛\(P\)的联络形式\(
abla\)必须满足非交换Bianchi恒等式扩展式\[
abla\wedge \star_H F + [A, F]^{⋆} = \mathcal{Q}_{RR} \],这里\(\star_H\)表示Hodge星算子在NS-NS场\(H_3\)存在时的修正形式,而\(\mathcal{Q}_{RR}\)对应RR荷的量子修正项。这种非交换规范结构导致D膜位形空间的量子化必须通过Gelfand-Naimark-Segal构造实现,其C*代数表示精确对应着膜宇宙场景中的全息对偶关系。
非交换几何框架下的曲率演化方程揭示了D膜拓扑稳定性与Calabi-Yau模空间的深层关联。考虑复三维Calabi-Yau流形\(M\)的Kähler参数空间\(\mathcal{M}_K\),D膜位形的量子涨落被编码在主丛曲率张量\(F\)的协变导数项中,满足修正的Yang-Mills方程\[ D_{⋆}F = j_B \]其中流项\(j_B\)来源于B场拓扑荷的Hodge对偶。这种表述成功统一了IIB型弦论中D3膜位形的S-对偶变换群作用,其解空间维度由流形Euler数\(\chi(M)\)与膜缠绕数的K理论类共同决定。
通过发展非交换联络的谱序列分析法,D膜在量子化背景下的动力学获得严格数学描述。将Calabi-Yau流形的复结构模空间\(\mathcal{M}_C\)与D膜位形空间\(\mathcal{B}_D\)建立纤维丛对应,其结构群\(G\)由规范对称性SU(N)与非交换参数空间的自同构群半直积构成。该框架下,D膜拓扑涨落的量子化条件等价于Deligne-Beilinson上同调类在非交换变形中的不变性,这为解释弦论真空选择机制中的模稳定性问题提供了新途径。
第三章 D膜拓扑动力学的几何表征与方程推导
3.1 基于纤维丛理论的D膜拓扑形变几何模型
在纤维丛理论框架下构建D膜拓扑形变的几何模型,需将规范场论与微分几何工具深度融合。D膜在Calabi-Yau流形上的位形演化本质上对应于主丛截面的动力学过程,其中规范群G的主丛P通过投影映射π:M→M/G与基底流形形成纤维化结构。该模型中,D膜拓扑形变的自由度被编码在联络形式A的规范等价类中,其曲率张量F=dA+A∧A精确表征了膜位形在纤维方向上的拓扑涨落。
关键突破在于建立规范主丛的拓扑形变与D膜缠绕数的对应关系。选取SU(N)结构群的主丛P,其伴随丛adP的截面空间Γ(adP)对应D膜开弦端点的规范自由度。当D膜沿流形M的p+1闭链Σ发生拓扑形变时,联络形式A的规范变换生成元必须满足整数量子化条件\[ \frac{1}{2π}\int_Σ Tr(F^k) ∈ \mathbb{Z} \],这保证了不同缠绕态之间的拓扑不连续性。特别地,当底流形存在非平凡的第二陈类c₂(M)时,主丛的拓扑分类由微分同胚群Diff(M)在Deligne上同调群H²(M,Ω¹→Ω²)上的作用决定,这为D膜拓扑稳定性提供了严格的几何判据。
模型的核心方程源于纤维丛曲率与D膜拓扑荷的动力学平衡。通过引入修正的Bianchi恒等式\[ D_H F = j_{RR} \],其中H为NS-NS场强对应的扭结类,j_{RR}表示RR荷的Hodge对偶流,该方程成功统一了D膜位形的拓扑约束与规范对称性要求。在此框架下,D膜拓扑形变的运动学由主丛上的Atiyah-Segal联络方程控制:\[ \bar{\partial}_A ψ + [Φ, ψ] = 0 \],其中ψ∈Γ(EndE)表征膜位形偏离平衡态的形变模量,Φ为超势函数诱导的Higgs场。该方程解空间维度由流形Hodge数h^{p,0}(M)与主丛Chern类的交点数共同决定。
此几何模型在三个层面超越传统理论:首先,主丛的Spin^c结构自然消除了开弦反常,通过微分形式的积分条件\[ \int_{Σ_{2k}} ch(E) ∧ \sqrt{\hat{A}(TΣ)} ∈ \mathbb{Z} \]实现量子反常的几何化消除;其次,规范主丛的模空间紧致化将D膜不同缠绕态统一在单参数纤维丛族中,解决了非交换几何背景下拓扑涨落的参数化难题;最后,通过发展纤维化流形的曲率演化方程,成功建立了D膜拓扑稳定性与Calabi-Yau模空间参数变形的严格对应关系,为研究弦论真空选择机制提供了新的数学工具。
3.2 Witten型拓扑流方程在D膜动力学中的几何实现
在D膜拓扑动力学的几何框架中,Witten型拓扑流方程的引入为描述膜位形演化提供了本质的守恒律结构。基于超对称拓扑场论的核心思想,将D膜世界体的规范场强\(F_{μν}\)与背景几何的曲率形式耦合,可构造具有微分同胚不变性的守恒流方程。该方程的核心几何实现体现在将D膜拓扑荷的动力学演化编码为规范主丛上闭链的协变导数方程。
通过建立主丛\(P(M,G)\)的联络形式\(A\)与D膜位形参数化空间\(\mathcal{M}_D\)的映射关系,Witten型方程呈现为曲率张量的Hodge对偶条件:\[ \star_H (F ∧ \Psi) = d_A \mathcal{J} \] 其中\(\Psi\)为Calabi-Yau流形特殊几何结构诱导的校准形式,\(\mathcal{J}\)表征RR荷流密度。该方程本质反映了D膜世界体上拓扑荷密度\(\rho_{top}=Tr(F∧F)\)与背景时空B场扭结类\([H_3]\)的动力学平衡,其积分形式对应着缠绕数守恒定律\[ \frac{d}{dt}\int_{Σ_{p+1}} \rho_{top} = \oint_{\partial Σ} \mathcal{J} \] 这种表述成功将D膜拓扑涨落约束转化为纤维丛截面空间的闭链条件。
关键突破在于发展出具有超对称不变性的修正联络方程。考虑D膜开弦端点激发的费米子自由度,引入超对称变换参数\(\epsilon\)生成的世界体超流\(S_μ=Tr(\epsilonγ_μλ)\),其中λ为gaugino场。此时Witten方程扩展为\[
abla_{[μ}S_{ν]} = \frac{1}{4}R_{μνρσ}γ^{ρσ}\epsilon + \frac{i}{2}H_{μνρ}γ^ρ\epsilon \] 该式将D膜位形的超对称条件与背景流形曲率张量\(R_{μνρσ}\)及NS-NS场强\(H_3\)建立严格对应,其解空间维度由流形Yau定理约束的Kähler模参数决定。
在具体几何实现中,D膜缠绕数量子化条件通过Atiyah-Patodi-Singer边界条件自然导出。当D膜沿Calabi-Yau流形的Lagrangian子流形\(L\)缠绕时,规范主丛的拓扑不变量满足\[ \int_L ch(V) ∧ e^{B} = \sqrt{\hat{A}(TL)} \] 其中\(ch(V)\)为规范丛陈特征,B场修正项确保方程在T对偶变换下的协变性。该条件在微分几何层面等价于要求主丛联络在子流形法丛方向满足自对偶条件,从而保证膜位形在量子涨落下保持拓扑稳定性。
此理论框架的优越性体现在三个层面:首先,通过Hodge理论将拓扑流守恒律与D膜位形参数化直接关联,克服了传统微扰方法在非紧致流形上的发散困难;其次,超对称扩展方程成功统一了玻色自由度与费米自由度的几何约束,为研究D膜量子涨落提供严格数学基础;最后,基于校准几何的积分条件为不同维度D膜间的对偶变换建立了不变量体系,显著提升了理论在膜宇宙场景中的预测能力。这些进展标志着D膜动力学研究从传统拓扑分类向微分几何深层结构的实质性跨越。
第四章 微分几何框架下D膜拓扑动力学的理论突破与未来展望
在微分几何框架下构建的D膜拓扑动力学理论体系,成功解决了传统弦论模型在非微扰区域的若干基础性难题。理论突破的核心体现在规范主丛结构与Calabi-Yau几何的深度融合:通过建立主丛曲率张量与D膜缠绕数的非线性对应关系,首次实现了非交换几何背景下拓扑涨落的协变量子化描述。这一进展不仅完善了IIB型弦论中D膜动力学的数学基础,更为重要的是揭示了规范场论与微分几何在量子引力层面的本质联系。
理论体系的创新性具体表现在三个维度。首先,基于Atiyah-Singer指标定理发展的纤维丛分类法,将D膜位形空间与靶流形的Deligne-Mumford紧化模空间建立严格对应,解决了不同缠绕态间的拓扑跃迁参数化问题。其次,通过引入修正的Bianchi恒等式\[ D_{⋆}F = j_{RR} + \mathcal{Q}_{top} \],其中\(\mathcal{Q}_{top}\)表征拓扑荷的量子修正项,统一了经典规范动力学与量子反常消除条件。最后,发展出具有超对称不变性的Witten型曲率流方程,将D膜位形演化转化为规范主丛上的参数化模空间遍历过程,其解空间的维度由Calabi-Yau流形的Hodge数精确约束。
在物理预言层面,该理论框架展现出独特优势。通过分析主丛联络的Spin^c结构约束,成功导出膜宇宙场景中紧化维度数与规范群秩次的对应关系,为解释标准模型规范对称性的几何起源提供了新思路。特别值得注意的是,基于Kähler-Ricci流建立的膜位形稳定性判据,揭示了弦真空简并性破缺与背景流形曲率演化的动力学关联,这为研究早期宇宙的时空相变机制开辟了新的理论路径。
未来研究将沿着三个方向深化现有成果。在数学基础层面,需进一步发展非交换上同调理论在弦论中的应用,特别是解决高亏格Calabi-Yau流形上D膜缠绕模式的Gromov-Witten不变量的计算问题。物理应用方面,应重点探索该几何框架在AdS/CFT对偶中的实现形式,建立D膜拓扑动力学与共形场论算子谱的严格对应。技术方法上,亟需开发基于张量网络的曲率流方程数值算法,以处理非紧致流形上膜位形量子涨落的非微扰计算。这些进展将推动微分几何方法与量子引力理论的深度融合,最终为揭示时空微观结构的几何本质提供关键理论工具。
参考文献
[1] 郑照明.SNAD生物膜厌氧氨氧化活性的氨氮抑制动力学研究[J].《中国环境科学》,2016年第10期2957-2963,共7页
[2] 崔英俊.马铃薯淀粉膜制备工艺优化及活性包装中百里香酚释放动力学[J].《农业工程学报》,2024年第20期298-308,共11页
[3] 乔贵民.腐蚀介质在缓蚀剂膜中扩散行为的分子动力学模拟[J].《物理化学学报》,2010年第11期3041-3046,共6页
[4] 李志锋.二氯卡宾与甲醇及甲硫醇反应的拓扑积分和热力学与动力学性质[J].《天水师范学院学报》,2009年第2期59-61,共3页
[5] 熊桂慧.D201树脂吸附SO_42-的动力学、热力学特性及表征分析[J].《精细化工》,2015年第11期1243-1247,共5页
通过本文的《超弦理论论文写作指南》与范文解析,您已掌握构建严谨理论框架的核心方法论。立即实践这些技巧,让复杂的弦论研究在清晰逻辑中展现科学之美,为探索宇宙本质的学术征程注入专业表达力。



